Cydonia


The Cydonia debate rages on. The orthodox view is that all of the features of the "Cydonia Mensae" are natural geological formations. This is the official view of NASA and most planetary astronomers. Although perhaps not everyone's true belief, no one ever lost a government grant by following traditional thinking. The "alternative theorists" however, have a drastically different point of view with regard to the objects in Cydonia; namely that they were created by some ancient extraterrestrial civilization. I have read many of the arguments from the latter camp and, frankly, do not find many of them particularly convincing (although see [1] for some excellent and more rigorous evidence.) We have all had the Rorschach experience of seeing familiar objects in clouds or rock formations. It is the brain's comforting way of finding the familiar in the unfamiliar. And yet, there is something different about Cydonia. The whole complex of mountains or geological structures looks unnatural. Certain objects appear to have a symmetry that can't be found elsewhere. My objective with this paper was to determine whether the Cydonia objects fall into the category of random rock formations that just happen to look artificial or do they exhibit such a high level of symmetry and uniformity that it is unlikely that they were naturally formed. I used objective statistical techniques to answer the question. My conclusion was unsettling; I see no alternative but that "The Face" is not a natural geological formation.
BACKGROUND For those new to the topic, Cydonia is a region of Mars, located in that planets Northern hemisphere at about 40.86°N, 9.91°W, according to latitude and longitude conventions. The controversy surrounding that region began in July of 1976 when the Viking orbiter spacecraft took the picture shown in Figure 1 (frame #35A72.) NASA released the photograph a few days later, somewhat as a publicity stunt, dismissing the face as a "trick of light and shadow" when shown to journalists at the Jet Propulsion Laboratory (JPL) in Pasadena, California. Their explanation for the face was that the geometry of the terrain combined with a lighting effect from the sun being low in the sky created shadows that made the 1.5-mile long hill resemble a face. The image was forgotten about for a few years until 1979, when two computer engineers at NASA's Goddard Space Flight Center, Vincent DiPietro and Gregory Molenaar, became intrigued by it and developed some image enhancing software to improve the quality of the photo. Discovering another curious 5-sided pyramid-shaped object nearby (now known as the "D&M Pyramid" in their honor), they presented their findings to a disinterested scientific establishment.		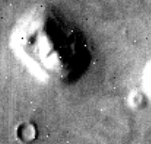	figure 1
Former NASA consultant and science advisor to CBS during the Apollo missions, Richard Hoagland picked up on the controversy and further developed the theory of Martian Monuments, having discovered the so-called "City" and "Fortress" (see Mars Global Surveyor (MGS) image in Figure 2 below).
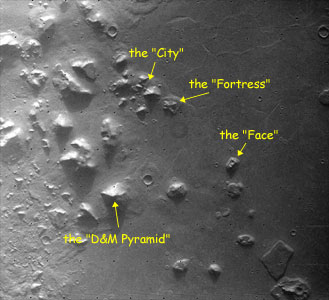figure 2		In 1987, Dr. Mark J. Carlotto, furthered the research by discovering possible "teeth" in the face and an overall symmetry of the face and its consistent appearance under a variety of lighting conditions (see his website "New Frontiers in Science," for a paper on the subject.) He called for NASA to utilize the 1992 spacecraft Mars Observor to re-image the area. Unfortunately, the mission was a bust and failed before getting into Mars orbit.
		In 1998, NASA's Mars Global Surveyor began imaging Mars and made some photos of the region that showed the face 20 years later and under different lighting conditions. The image in Figure 3, for example, was taken under cloudless conditions on 8 April 2001 and has a resolution of 1.56 meters per pixel. For many, this image ended the debate since it no longer looks like a face.	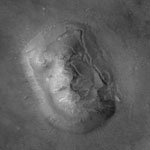figure 3
However, it is actually this image that led me to want to do this investigation. It shows a fairly clear outline of the object and it is this outline that intrigues me the most. At a glance, the left side of the face looks like a fairly straight line. The right side is also straight, except for a couple bumps that could easily be due to erosion or partial coverage by sand or dust. The upper and lower edges of the face also seem unaturally smooth; circular or elliptic. So one wonders; what are the odds of a natural geological feature showing such smooth edges and symmetry? There are at least 4 anomalies that I find "unnatural" about the Cydonia face and its neighbors in the region: 1. The symmetry of the face 2. The smoothness of the edges of the face 3. The fact that it resembles a face 4. The fact that it resides within a region of a number of other curious structures Let us consider the probability of each of these anomalies occurring in nature. Let p(s) represent the probability that a geological structure would have the level of symmetry of The Face. Let p(e) represent the probability that a geological structure would have edges as smooth as The Face. Let p(f) represent the probability that a geological structure would look like a face or some other obviously recognizable object. Let p(c) represent the probability that a geological structure would reside in a region of other similarly unnatural objects.
Then the probability P that The Face is natural would be P=p(s)p(e)p(f)p(c)*. The reason that I multiply all of these probabilities is because The Face has all of the anomalies mentioned above. For example, Figure 4a shows a shape that is simply symmetrical. Figure 4b shows a shape that has smooth edges but is not symmetrical. One can also imagine a shape that resembles a face but is neither symmetrical nor has smooth edges (like the kind you see in clouds). The Face has all of these unusual characteristics, and so, in order to find the probability of such a structure occurring naturally, one has to multiply the probabilities of each anomaly. Finally, The Face could be sitting by itself in some region of Mars that has no other unusual characteristics. The odds of that are nearly 1. However, it is not; it sits in the region of a number of other very unusual shapes, which lowers even further the likelihood that it is natural. As we will see, we do not have to go far with this argument to prove the unliklihood of The Face being natural. Let's consider the smooth edge probability first...			figure 4
			figure 4
THE PROBABILITY OF STRAIGHT OR SMOOTH EDGES What does it mean for an edge to be straight? How do you define straight? Straightness can be defined as the amount of deviation side-to-side over a particular distance. For example, in Figure 5a the blue line is only 5 times as long as its deviation in width and is bound by a red rectangle that is 5 times longer than it is wide. One could define a straightness factor S as length divided by the deviation in width. Figure 5a, then has a straightness of 5. The line in Figure 5b has a straightness of 13, because the red bounding rectangle has a length to width ratio of 13. In nature, there are few things that have naturally occuring smooth edges. One is a crater, which is generally round because the width of the impact crater is much larger than the object that created it. Another would be a gorge created by a glacier or a channel created by fast running water. However, protruding objects, like mountains and islands have a random shape to them. The Face, on the other hand, is a protruding object with a shape like the red outline in Figure 6. That outline was created using straight lines for the left and right sides and ellipse segments for the top and bottom. The ellipse segments were slightly skewed using a standard Adobe Photoshop 7.0 transformation to compensate for the perspective angle of image. The questions are: 1. How straight are the edges of The Face? 2. How closely do the top and bottom of the image match a true ellipse? 3. How probable is this in nature? If we accept that an edge of a protruding object in nature is random, it can be modeled with a random walk. A random walk would be a path taken where each step in the path is in a random direction from the previous point. This won't exactly model a natural object like a mountain because such objects close on themselves, which limits a large set of random walks. However, I will hypothesize that the probability of finding a straight edge on a protruding object in nature is approximately equivalent to a random walk subject to the constraint that the path never reverses direction. We can test this theory against actual data, once we have determined the probabilities for edges of various straightness factors.			figure 5a figure 5b
			figure 6
figure 7	To determine probabilities, consider the grid shown in Figure 7. There are 9 points on the grid. Consider the random walk to start at point 2 (yellow dot), with the objective being to reach the line 7-8-9. The walk can take 1 step at a time and can only move up, to the left, or to the right. After the first step, for example, the position of the yellow dot would either be 1, 3, or 5, with an equal probability of landing at each of those (.333). From point 1, the 2nd step would land at either 2, 4, or outside the grid, again each with equal probability. Landing outside the grid means that the random walk failed to stay within the grid. From point 5, the 2nd step would land at either 4, 6, or 8. Landing at 7, 8, or 9 means that the random walk succeeded through the grid. If we iterate this process an infinite number of times, we will find that the walk will reach point 8 about 22.4% of the time without stepping outside of the grid. It will land at points 7 or 9 about 12.2% of the time each , and will fail to make it through the grid about 53.2% of the time.
If, instead of starting at point 2, we start the random walk at point 1 (point 3 will have an analogous result), the walk will reach point 8 about 21.7% of the time, points 7 or 9 about 8.8% of the time each, and will fail to make it through the grid about 61.1% of the time. We can then extend the analysis to grids that have a 2:1 length to width ratio by iterating the random walk. The net result is shown in charts 8a and 8b. From 8a, we see that a random walk occurs through a 2:1 grid about 20% of the time, and a 3:1 grid about 8% of the time. The latter corresponds to the likelihood of an edge occuring in nature with a straightness factor of 3. As can be seen, the straighter the edge, the less likely it would occur. Past a straightness of 6, the probabilities are so low that we need to plot them on the logarithmic chart shown in Figure 8b. Here we see, for example, that for a random walk, or a straight line, to occur in nature with a straightness of 20, the odds are less than 1 in 10 MILLION!
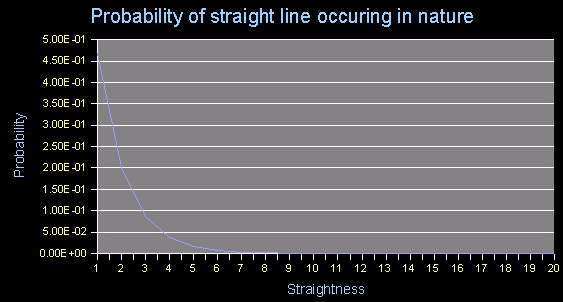figure 8a
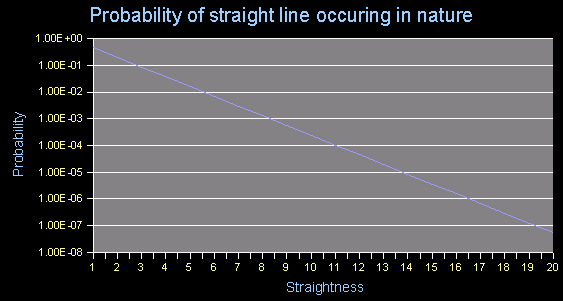figure 8b
I would also argue that this analysis applies equally well to curved edges that follow mathematical properties, e.g. an arc of a circle or a segment of an ellipse. For example, if the perimeter of an elliptical edge were 20 times the maximum deviation perpendicular to the direction of the edge, then it would be just as likely to occur in nature as a straight edge with a similar ratio. Again, this would not apply to naturally occuring circles, such as craters, but, rather, to protruding objects like mountains that follow random edge properties. HOW STRAIGHT/SMOOTH (IMPROBABLE) IS THE FACE? Now we can ask the question: How straight or smooth is the outline of The Face? To do this, I took the April 2001 MGS image shown in Figure 3 above, as it has the best resolution and therefore the most well defined edges. Figure 9a shows a closeup of The Face. In Figure 9b, I traced the outline of the border as closely as I could. Figure 9c shows how this outline compares to an approximate border composed of straight lines and segments of an ellipse.
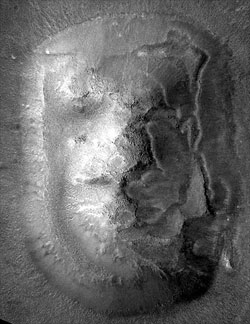figure 9a		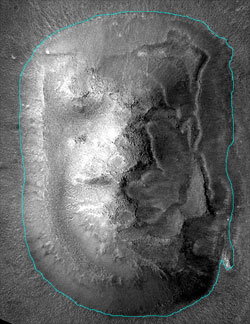figure 9b
	figure 9c
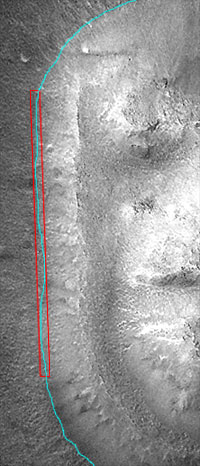figure 10	Figure 10 shows a bounding rectangle around the left side edge. The bounding rectangle has a straighness ratio of 35:1, which gives it a probability of occuring in nature of 2E-13, or 2 in 10 thousand trillions. The right side turns out to have a straightness of 23:1, which corresponds to a probability of 5E-9 or 5 in a billion. Using the same technique for the top edge, considering the length to be the length of the elliptical segment, it has an "elliptical smoothness" of about 20:1, for a probability of 5 in 100 million. The bottom edge, because of the blip in the lower right, has a smoothness of about 15:1, for a probability of 4 in a million. To find the overall probability of a shape occuring that has all 4 edges with the corresponding smoothnesses, we need to multiply all probabilities, for a net probability of 1.5E-34. This, of course, is an unimaginably small number. But, still, to determine the likelihood of an object like this occuring naturally on Mars, we have to ask the question: "How many protruding objects (mountains, hills, etc.) are there on Mars?" If there were 1E34, then the odds of finding at least one with such a smooth shape would be about 50-50. We know the answer, of course, but lets do the math for the sake of completeness. I randomly selected 20 MGS images from Charts 4, 5, 20, 23, and 25, and examined them for well defined objects. Unfortunately, there are very few. Mars has great expanses of flat desert-looking regions, punctuated only by craters. Where there are mountain ranges, they tend to be ill-defined; typically large ranges with ridges and sand or dust covering much of the base. Cydonia is fairly unique in having a number of objects set neatly on a flat surface. The 20 randomly selected charts represent a total of 4600 square km. In these charts, there were only about 30 well defined objects. The entire surface of Mars is 580 million square km. Therefore, if the charts analyzed were representative of the number of well defined objects throughout the planet, a good estimate would be: Total Number of Objects = 5.8E8 * 30 / 4600 or 3.8 million.
Let's consider this to be the lower bound. For an upper bound, we could assume that there is an object the size of The Face every few miles, such that well defined objects actually comprise 10% of the surface area of the planet (just looking at the charts, it is easy to see that this upper bound is highly unrealistic). In that case, since the face covers about 5 sq. km, there would be (5.8E8 / 5)/10, or about 12 million objects. Even taking the upper bound, the probability of just one of those 12 million objects having an shape as smooth and symmetrical as The Face would be 1.5E-34 * 1.2E7 = 1.8E-27. So p(e) = 1.8E-27. Since this probability is so unimaginably small, and since none of the other probabilities can be greater than one, the overall probability P that The Face is a natural formation must be less than 1.8E-27. Therefore, it seems clear that The Face was artificially created. I welcome any and all feedback to this argument (please email me), especially any that point out a flaw in my calculations or logic. Otherwise, the conclusion is both very interesting and somewhat disturbing. MORE ON MARS Footnotes: [1] T. Van Flandern, M. Carlotto, H. Crater, J. Erjavec, L. Fleming, J.P. Levasseur "Evidence of Planetary Artifacts"

	©2002-2003 Jim Elvidge. All rights reserved.